The value of the derivative of the function at the point is equal to. Find the value of the derivative of the function at the point x0

11.10.2019

It is absolutely impossible to solve physical problems or examples in mathematics without knowledge about the derivative and methods for calculating it. The derivative is one of the most important concepts of mathematical analysis. We decided to devote today's article to this fundamental topic. What is a derivative, what is its physical and geometric meaning, how to calculate the derivative of a function? All these questions can be combined into one: how to understand the derivative?

Geometric and physical meaning of the derivative

Let there be a function f(x) , given in some interval (a,b) . The points x and x0 belong to this interval. When x changes, the function itself changes. Argument change - difference of its values x-x0 . This difference is written as delta x and is called argument increment. The change or increment of a function is the difference between the values of the function at two points. Derivative definition:

The derivative of a function at a point is the limit of the ratio of the increment of the function at a given point to the increment of the argument when the latter tends to zero.

Otherwise it can be written like this:

What is the point in finding such a limit? But which one:

the derivative of a function at a point is equal to the tangent of the angle between the OX axis and the tangent to the graph of the function at a given point.

physical meaning derivative: the time derivative of the path is equal to the speed of the rectilinear motion.

Indeed, since school days, everyone knows that speed is a private path. x=f(t) and time t . average speed for some period of time:

To find out the speed of movement at a time t0 you need to calculate the limit:

Rule one: take out the constant

The constant can be taken out of the sign of the derivative. Moreover, it must be done. When solving examples in mathematics, take as a rule - if you can simplify the expression, be sure to simplify .

Example. Let's calculate the derivative:

Rule two: derivative of the sum of functions

The derivative of the sum of two functions is equal to the sum of the derivatives of these functions. The same is true for the derivative of the difference of functions.

We will not give a proof of this theorem, but rather consider a practical example.

Find the derivative of a function:

Rule three: the derivative of the product of functions

The derivative of the product of two differentiable functions is calculated by the formula:

Example: find the derivative of a function:

Solution:

Here it is important to say about the calculation of derivatives of complex functions. The derivative of a complex function is equal to the product of the derivative of this function with respect to the intermediate argument by the derivative of the intermediate argument with respect to the independent variable.

In the above example, we encounter the expression:

In this case, the intermediate argument is 8x to the fifth power. In order to calculate the derivative of such an expression, we first consider the derivative of the external function with respect to the intermediate argument, and then multiply by the derivative of the intermediate argument itself with respect to the independent variable.

Rule Four: The derivative of the quotient of two functions

Formula for determining the derivative of a quotient of two functions:

We tried to talk about derivatives for dummies from scratch. This topic is not as simple as it sounds, so be warned: there are often pitfalls in the examples, so be careful when calculating derivatives.

With any question on this and other topics, you can contact the student service. Per short term we will help you solve the most difficult test and deal with tasks, even if you have never dealt with the calculation of derivatives before.

The operation of finding a derivative is called differentiation.

As a result of solving problems of finding derivatives of the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716) were the first to work in the field of finding derivatives.

Therefore, in our time, in order to find the derivative of any function, it is not necessary to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but only need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.

To find the derivative, you need an expression under the stroke sign break down simple functions and determine what actions (product, sum, quotient) these functions are related. Further, we find the derivatives of elementary functions in the table of derivatives, and the formulas for the derivatives of the product, sum and quotient - in the rules of differentiation. The table of derivatives and differentiation rules are given after the first two examples.

Example 1 Find the derivative of a function

Solution. From the rules of differentiation we find out that the derivative of the sum of functions is the sum of derivatives of functions, i.e.

From the table of derivatives, we find out that the derivative of "X" is equal to one, and the derivative of the sine is cosine. We substitute these values in the sum of derivatives and find the derivative required by the condition of the problem:

Example 2 Find the derivative of a function

Solution. Differentiate as a derivative of the sum, in which the second term with a constant factor, it can be taken out of the sign of the derivative:

If there are still questions about where something comes from, they, as a rule, become clear after reading the table of derivatives and the simplest rules of differentiation. We are going to them right now.

Table of derivatives of simple functions

1. Derivative of a constant (number). Any number (1, 2, 5, 200...) that is in the function expression. Always zero. This is very important to remember, as it is required very often
2. Derivative of the independent variable. Most often "x". Always equal to one. This is also important to remember
3. Derivative of degree. When solving problems, you need to convert non-square roots to a power.
4. Derivative of a variable to the power of -1
5. Derivative square root
6. Sine derivative
7. Cosine derivative
8. Tangent derivative
9. Derivative of cotangent
10. Derivative of the arcsine
11. Derivative of arc cosine
12. Derivative of arc tangent
13. Derivative of the inverse tangent
14. Derivative of natural logarithm
15. Derivative of a logarithmic function
16. Derivative of the exponent
17. Derivative of exponential function

Differentiation rules

1. Derivative of the sum or difference
2. Derivative of a product
2a. Derivative of an expression multiplied by a constant factor
3. Derivative of the quotient
4. Derivative of a complex function

Rule 1If functions

are differentiable at some point , then at the same point the functions

and

those. the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions.

Consequence. If two differentiable functions differ by a constant, then their derivatives are, i.e.

Rule 2If functions

are differentiable at some point , then their product is also differentiable at the same point

and

those. the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other.

Consequence 1. The constant factor can be taken out of the sign of the derivative:

Consequence 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each of the factors and all the others.

For example, for three multipliers:

Rule 3If functions

differentiable at some point and , then at this point their quotient is also differentiable.u/v , and

those. the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator.

Where to look on other pages

When finding the derivative of the product and the quotient in real problems, it is always necessary to apply several differentiation rules at once, so more examples on these derivatives are in the article."The derivative of a product and a quotient".

Comment. You should not confuse a constant (that is, a number) as a term in the sum and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. it typical mistake, which occurs on initial stage learning derivatives, but as they solve several one-two-component examples, the average student no longer makes this mistake.

And if, when differentiating a product or a quotient, you have a term u"v, wherein u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (such a case is analyzed in example 10).

Another common mistake is the mechanical solution of the derivative of a complex function as the derivative of a simple function. That's why derivative of a complex function is devoted separate article. But first we will learn to find derivatives of simple functions.

Along the way, you can not do without transformations of expressions. To do this, you may need to open in new windows manuals Actions with powers and roots and Actions with fractions .

If you are looking for solutions to derivatives with powers and roots, that is, when the function looks like , then follow the lesson " Derivative of the sum of fractions with powers and roots".

If you have a task like , then you are in the lesson "Derivatives of simple trigonometric functions".

Step by step examples - how to find the derivative

Example 3 Find the derivative of a function

Solution. We determine the parts of the expression of the function: the entire expression represents the product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the product differentiation rule: the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other:

Next, we apply the rule of differentiation of the sum: the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum, the second term with a minus sign. In each sum, we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, "x" turns into one, and minus 5 - into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We get the following values of derivatives:

We substitute the found derivatives into the sum of products and obtain the derivative of the entire function required by the condition of the problem:

Example 4 Find the derivative of a function

Solution. We are required to find the derivative of the quotient. We apply the formula for differentiating a quotient: the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator. We get:

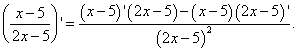
We have already found the derivative of the factors in the numerator in Example 2. Let's also not forget that the product, which is the second factor in the numerator in the current example, is taken with a minus sign:

If you are looking for solutions to such problems in which you need to find the derivative of a function, where there is a continuous pile of roots and degrees, such as, for example, then welcome to class "The derivative of the sum of fractions with powers and roots" .

If you need to learn more about derivatives of sines, cosines, tangents and others trigonometric functions, that is, when the function looks like , then you have a lesson "Derivatives of simple trigonometric functions" .

Example 5 Find the derivative of a function

Solution. In this function, we see a product, one of the factors of which is the square root of the independent variable, with the derivative of which we familiarized ourselves in the table of derivatives. According to the product differentiation rule and the tabular value of the derivative of the square root, we get:

Example 6 Find the derivative of a function

Solution. In this function, we see the quotient, the dividend of which is the square root of the independent variable. According to the rule of differentiation of the quotient, which we repeated and applied in example 4, and the tabular value of the derivative of the square root, we get:

To get rid of the fraction in the numerator, multiply the numerator and denominator by .

Example 1

Reference: The following ways of notating a function are equivalent: In some tasks, it is convenient to designate the function as a “player”, and in some as “ef from x”.

First we find the derivative:

Example 2

Calculate the derivative of a function at a point

, , full function study and etc.

Example 3

Calculate the derivative of the function at the point . Let's find the derivative first:

Well, that's a completely different matter. Calculate the value of the derivative at the point :

In the event that you do not understand how the derivative was found, return to the first two lessons of the topic. If there are difficulties (misunderstanding) with the arc tangent and its meanings, necessarily study methodical material Graphs and properties of elementary functions- the very last paragraph. Because there are still enough arctangents for the student age.

Example 4

Calculate the derivative of the function at the point .

The equation of the tangent to the graph of the function

To consolidate the previous paragraph, consider the problem of finding the tangent to function graphics at this point. We met this task at school, and it is also found in the course of higher mathematics.

Consider a "demonstration" elementary example.

Write an equation for the tangent to the graph of the function at the point with the abscissa. I will immediately give a ready-made graphical solution to the problem (in practice, this is not necessary in most cases):

A rigorous definition of a tangent is given by definitions of the derivative of a function, but until we master technical part question. Surely almost everyone intuitively understands what a tangent is. If you explain "on the fingers", then the tangent to the graph of the function is straight, which concerns the graph of the function in the only point. In this case, all nearby points of the straight line are located as close as possible to the graph of the function.

As applied to our case: at , the tangent (standard notation) touches the graph of the function at a single point.

And our task is to find the equation of a straight line.

Derivative of a function at a point

How to find the derivative of a function at a point? Two obvious points of this task follow from the wording:

1) It is necessary to find the derivative.

2) It is necessary to calculate the value of the derivative at a given point.

Example 1

Calculate the derivative of a function at a point

Help: The following ways of notating a function are equivalent:

In some tasks, it is convenient to designate the function as a “player”, and in some as “ef from x”.

First we find the derivative:

I hope that many have already adapted to find such derivatives orally.

At the second step, we calculate the value of the derivative at the point :

A small warm-up example for an independent solution:

Example 2

Calculate the derivative of a function at a point

Full solution and answer at the end of the lesson.

The need to find the derivative at a point arises in the following tasks: constructing a tangent to the graph of a function (next paragraph), study of a function for an extremum , study of the function for the inflection of the graph , full function study and etc.

But the task in question occurs in control work and by itself. And, as a rule, in such cases, the function is given quite complex. In this regard, consider two more examples.

Example 3

Calculate the derivative of a function at point .
Let's find the derivative first:

The derivative, in principle, is found, and the required value can be substituted. But I don't really want to do anything. The expression is very long, and the value of "x" is fractional. Therefore, we try to simplify our derivative as much as possible. In this case, let's try to reduce the last three terms to a common denominator: at point .

This is a do-it-yourself example.

How to find the value of the derivative of the function F(x) at the Ho point? How to solve it in general?

If the formula is given, then find the derivative and substitute X-zero instead of X. count
If a we are talking o b-8 USE, graph, then you need to find the tangent of the angle (acute or obtuse), which forms a tangent to the X axis (using the mental construction of a right triangle and determining the tangent of the angle)

Timur adilkhodzhaev

First, you need to decide on the sign. If the point x0 is in the lower part of the coordinate plane, then the sign in the answer will be minus, and if it is higher, then +.
Secondly, you need to know what is tange in a rectangular rectangle. And this is the ratio of the opposite side (leg) to the adjacent side (also leg). There are usually a few black marks on the painting. From these marks you make right triangle and find tanges.

How to find the value of the derivative of the function f x at the point x0?

there is no specific question - 3 years ago

In the general case, in order to find the value of the derivative of a function with respect to some variable at any point, it is necessary to differentiate the given function with respect to this variable. In your case, by the variable X. In the resulting expression, instead of X, put the value of x at the point for which you need to find the value of the derivative, i.e. in your case, substitute zero X and calculate the resulting expression.

Well, your desire to understand this issue, in my opinion, undoubtedly deserves +, which I put with a clear conscience.

Such a formulation of the problem of finding the derivative is often posed to fix the material on the geometric meaning of the derivative. A graph of a certain function is proposed, completely arbitrary and not given by an equation, and it is required to find the value of the derivative (not the derivative itself!) at the specified point X0. To do this, a tangent to the given function is constructed and the points of its intersection with the coordinate axes are found. Then the equation of this tangent is drawn up in the form y=kx+b.

In this equation, the coefficient k and will be the value of the derivative. it remains only to find the value of the coefficient b. To do this, we find the value of y at x \u003d o, let it be equal to 3 - this is the value of the coefficient b. We substitute the values of X0 and Y0 into the original equation and find k - our value of the derivative at this point.

If we follow the definition, then the derivative of a function at a point is the limit of the increment ratio of the function Δ y to the increment of the argument Δ x:

Everything seems to be clear. But try to calculate by this formula, say, the derivative of the function f(x) = x 2 + (2x+ 3) · e x sin x. If you do everything by definition, then after a couple of pages of calculations you will simply fall asleep. Therefore, there are simpler and more effective ways.

To begin with, we note that the so-called elementary functions can be distinguished from the whole variety of functions. These are relatively simple expressions, the derivatives of which have long been calculated and entered in the table. Such functions are easy enough to remember, along with their derivatives.

Derivatives of elementary functions

Elementary functions are everything listed below. The derivatives of these functions must be known by heart. Moreover, it is not difficult to memorize them - that's why they are elementary.

So, the derivatives of elementary functions:

Name	Function	Derivative
Constant	f(x) = C, C ∈ R	0 (yes, yes, zero!)
Degree with rational exponent	f(x) = x n	n · x n − 1
Sinus	f(x) = sin x	cos x
Cosine	f(x) = cos x	− sin x(minus sine)
Tangent	f(x) = tg x	1/cos 2 x
Cotangent	f(x) = ctg x	− 1/sin2 x
natural logarithm	f(x) = log x	1/x
Arbitrary logarithm	f(x) = log a x	1/(x ln a)
Exponential function	f(x) = e x	e x(nothing changed)

If an elementary function is multiplied by an arbitrary constant, then the derivative of the new function is also easily calculated:

(C · f)’ = C · f ’.

In general, constants can be taken out of the sign of the derivative. For example:

(2x 3)' = 2 ( x 3)' = 2 3 x 2 = 6x 2 .

Obviously, elementary functions can be added to each other, multiplied, divided, and much more. This is how new functions will appear, no longer very elementary, but also differentiable according to certain rules. These rules are discussed below.

Derivative of sum and difference

Let the functions f(x) and g(x), whose derivatives are known to us. For example, you can take the elementary functions discussed above. Then you can find the derivative of the sum and difference of these functions:

(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’

So, the derivative of the sum (difference) of two functions is equal to the sum (difference) of the derivatives. There may be more terms. For example, ( f + g + h)’ = f ’ + g ’ + h ’.

Strictly speaking, there is no concept of "subtraction" in algebra. There is a concept of "negative element". Therefore, the difference f − g can be rewritten as a sum f+ (−1) g, and then only one formula remains - the derivative of the sum.

f(x) = x 2 + sinx; g(x) = x 4 + 2x 2 − 3.

Function f(x) is the sum of two elementary functions, so:

f ’(x) = (x 2+ sin x)’ = (x 2)' + (sin x)’ = 2x+ cosx;

We argue similarly for the function g(x). Only there are already three terms (from the point of view of algebra):

g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).

Answer:
f ’(x) = 2x+ cosx;
g ’(x) = 4x · ( x 2 + 1).

Derivative of a product

Mathematics is a logical science, so many people believe that if the derivative of the sum is equal to the sum of the derivatives, then the derivative of the product strike"\u003e equal to the product of derivatives. But figs to you! The derivative of the product is calculated using a completely different formula. Namely:

(f · g) ’ = f ’ · g + f · g ’

The formula is simple, but often forgotten. And not only schoolchildren, but also students. The result is incorrectly solved problems.

A task. Find derivatives of functions: f(x) = x 3 cosx; g(x) = (x 2 + 7x− 7) · e x .

Function f(x) is a product of two elementary functions, so everything is simple:

f ’(x) = (x 3 cos x)’ = (x 3)' cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (−sin x) = x 2 (3cos x − x sin x)

Function g(x) the first multiplier is a bit more complicated, but general scheme this does not change. Obviously, the first multiplier of the function g(x) is a polynomial, and its derivative is the derivative of the sum. We have:

g ’(x) = ((x 2 + 7x− 7) · e x)’ = (x 2 + 7x− 7)' · e x + (x 2 + 7x− 7) ( e x)’ = (2x+ 7) · e x + (x 2 + 7x− 7) · e x = e x(2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x+ 9) · e x .

Answer:
f ’(x) = x 2 (3cos x − x sin x);
g ’(x) = x(x+ 9) · e x .

Note that in the last step, the derivative is factorized. Formally, this is not necessary, but most derivatives are not calculated on their own, but to explore the function. This means that further the derivative will be equated to zero, its signs will be found out, and so on. For such a case, it is better to have an expression decomposed into factors.

If there are two functions f(x) and g(x), and g(x) ≠ 0 on the set of interest to us, we can define a new function h(x) = f(x)/g(x). For such a function, you can also find the derivative:

Not weak, right? Where did the minus come from? Why g 2? But like this! This is one of the most complex formulas - you can’t figure it out without a bottle. Therefore, it is better to study it with specific examples.

A task. Find derivatives of functions:

There are elementary functions in the numerator and denominator of each fraction, so all we need is the formula for the derivative of the quotient:

By tradition, we factor the numerator into factors - this will greatly simplify the answer:

A complex function is not necessarily a formula half a kilometer long. For example, it suffices to take the function f(x) = sin x and replace the variable x, say, on x 2+ln x. It turns out f(x) = sin ( x 2+ln x) is a complex function. She also has a derivative, but it will not work to find it according to the rules discussed above.

How to be? In such cases, the replacement of a variable and the formula for the derivative of a complex function help:

f ’(x) = f ’(t) · t', if x is replaced by t(x).

As a rule, the situation with the understanding of this formula is even more sad than with the derivative of the quotient. Therefore, it is also better to explain it with specific examples, with detailed description every step.

A task. Find derivatives of functions: f(x) = e 2x + 3 ; g(x) = sin ( x 2+ln x)

Note that if in the function f(x) instead of expression 2 x+ 3 will be easy x, then we get an elementary function f(x) = e x. Therefore, we make a substitution: let 2 x + 3 = t, f(x) = f(t) = e t. We are looking for the derivative of a complex function by the formula:

f ’(x) = f ’(t) · t ’ = (e t)’ · t ’ = e t · t ’

And now - attention! Performing a reverse substitution: t = 2x+ 3. We get:

f ’(x) = e t · t ’ = e 2x+ 3 (2 x + 3)’ = e 2x+ 3 2 = 2 e 2x + 3

Now let's look at the function g(x). Obviously needs to be replaced. x 2+ln x = t. We have:

g ’(x) = g ’(t) · t' = (sin t)’ · t' = cos t · t ’

Reverse replacement: t = x 2+ln x. Then:

g ’(x) = cos( x 2+ln x) · ( x 2+ln x)' = cos ( x 2+ln x) · (2 x + 1/x).

That's all! As can be seen from the last expression, the whole problem has been reduced to calculating the derivative of the sum.

Answer:
f ’(x) = 2 e 2x + 3 ;
g ’(x) = (2x + 1/x) cos ( x 2+ln x).

Very often in my lessons, instead of the term “derivative”, I use the word “stroke”. For example, a stroke from the sum is equal to the sum strokes. Is that clearer? Well, that's good.

Thus, the calculation of the derivative comes down to getting rid of these very strokes according to the rules discussed above. As a final example, let's return to the derivative power with a rational exponent:

(x n)’ = n · x n − 1

Few know that in the role n may well act fractional number. For example, the root is x 0.5 . But what if there is something tricky under the root? Again, a complex function will turn out - they like to give such constructions in tests and exams.

A task. Find the derivative of a function:

First, let's rewrite the root as a power with a rational exponent:

f(x) = (x 2 + 8x − 7) 0,5 .

Now we make a substitution: let x 2 + 8x − 7 = t. We find the derivative by the formula:

f ’(x) = f ’(t) · t ’ = (t 0.5)' t' = 0.5 t−0.5 t ’.

We make a reverse substitution: t = x 2 + 8x− 7. We have:

f ’(x) = 0.5 ( x 2 + 8x− 7) −0.5 ( x 2 + 8x− 7)' = 0.5 (2 x+ 8) ( x 2 + 8x − 7) −0,5 .

Finally, back to the roots:

Derivative of a function of one variable.

Introduction.

Real methodological developments designed for students of the Faculty of Industrial and Civil Engineering. They are compiled in relation to the program of the course of mathematics in the section "Differential calculus of functions of one variable."

The developments are a single methodological guide, which includes: brief theoretical information; "typical" tasks and exercises with detailed solutions and explanations for these solutions; control options.

Additional exercises at the end of each paragraph. Such a structure of developments makes them suitable for independent mastery of the section with the most minimal assistance from the teacher.

§one. Definition of a derivative.

Mechanical and geometric meaning

derivative.

The concept of a derivative is one of the most important concepts of mathematical analysis. It arose as early as the 17th century. The formation of the concept of a derivative is historically associated with two problems: the problem of the speed of variable motion and the problem of a tangent to a curve.

These tasks, despite their various content, lead to the same mathematical operation that must be carried out on a function. This operation has received a special name in mathematics. It is called the operation of differentiating a function. The result of a differentiation operation is called a derivative.

So, the derivative of the function y=f(x) at the point x0 is the limit (if it exists) of the ratio of the increment of the function to the increment of the argument
at
.

The derivative is usually denoted as follows:
.

So by definition

The symbols are also used to denote the derivative
.

The mechanical meaning of the derivative.

If s=s(t) is the law of rectilinear motion of a material point, then
is the speed of this point at time t.

The geometric meaning of the derivative.

If the function y=f(x) has a derivative at a point , then slope tangent to the graph of a function at a point
equals
.

Example.

Find the derivative of a function
at the point =2:

1) Let's give a point =2 increment
. Notice, that.

2) Find the increment of the function at the point =2:

3) Compose the ratio of the increment of the function to the increment of the argument:

Let us find the limit of the relation at
:

In this way,
.

§ 2. Derivatives of some

the simplest functions.

The student needs to learn how to calculate the derivatives of specific functions: y=x,y= and in general y= .

Find the derivative of the function y=x.

those. (x)′=1.

Let's find the derivative of the function

Derivative

Let
then

It is easy to notice a pattern in the expressions for derivatives of a power function
at n=1,2,3.

Consequently,

. (1)

This formula is valid for any real n.

In particular, using formula (1), we have:

;

Example.

Find the derivative of a function

This function is a special case of a function of the form

at
.

Using formula (1), we have

Derivatives of functions y=sin x and y=cos x.

Let y=sinx.

Divide by ∆x, we get

Passing to the limit as ∆x→0, we have

Let y=cosx .

Passing to the limit as ∆x→0, we obtain

;
. (2)

§3. Basic rules of differentiation.

Consider the rules of differentiation.

Theorem1 . If the functions u=u(x) and v=v(x) are differentiable at a given point x, then their sum is also differentiable at this point, and the derivative of the sum is equal to the sum of the derived terms: (u+v)"=u"+v".(3 )

Proof: consider the function y=f(x)=u(x)+v(x).

The increment ∆x of the argument x corresponds to the increments ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) of the functions u and v. Then the function y will be incremented

∆y=f(x+∆x)-f(x)=

=--=∆u+∆v.

Consequently,

So, (u+v)"=u"+v".

Theorem2. If the functions u=u(x) and v=v(x) are differentiable at a given point x, then their product is also differentiable at the same point. In this case, the derivative of the product is found by the following formula: (uv) "=u" v + uv ". ( four)

Proof: Let y=uv, where u and v are some differentiable functions of x. Let x be incremented by ∆x; then u will be incremented by ∆u, v will be incremented by ∆v, and y will be incremented by ∆y.

We have y+∆y=(u+∆u)(v+∆v), or

y+∆y=uv+u∆v+v∆u+∆u∆v.

Therefore, ∆y=u∆v+v∆u+∆u∆v.

From here

Passing to the limit as ∆x→0 and taking into account that u and v do not depend on ∆x, we have

Theorem 3. The derivative of a quotient of two functions is equal to a fraction, the denominator of which is equal to the square of the divisor, and the numerator is the difference between the product of the derivative of the dividend by the divisor and the product of the dividend by the derivative of the divisor, i.e.

If a
then
(5)