Solution of the simplest trigonometric. Rules for finding trigonometric functions: sine, cosine, tangent and cotangent. Graph of the cosine function, y = cos x

The concepts of sine, cosine, tangent and cotangent are the main categories of trigonometry - a branch of mathematics, and are inextricably linked with the definition of an angle. Possession of this mathematical science requires memorization and understanding of formulas and theorems, as well as developed spatial thinking. That is why trigonometric calculations often cause difficulties for schoolchildren and students. To overcome them, you should become more familiar with trigonometric functions and formulas.

Concepts in trigonometry

To understand the basic concepts of trigonometry, you must first decide what a right triangle and an angle in a circle are, and why all basic trigonometric calculations are associated with them. A triangle in which one of the angles is 90 degrees is a right triangle. Historically, this figure was often used by people in architecture, navigation, art, astronomy. Accordingly, studying and analyzing the properties of this figure, people came to the calculation of the corresponding ratios of its parameters.

The main categories associated with right triangles are the hypotenuse and the legs. The hypotenuse is the side of a triangle that is opposite the right angle. The legs, respectively, are the other two sides. The sum of the angles of any triangle is always 180 degrees.

Spherical trigonometry is a section of trigonometry that is not studied at school, but in applied sciences such as astronomy and geodesy, scientists use it. A feature of a triangle in spherical trigonometry is that it always has a sum of angles greater than 180 degrees.

Angles of a triangle

In a right triangle, the sine of an angle is the ratio of the leg opposite the desired angle to the hypotenuse of the triangle. Accordingly, the cosine is the ratio of the adjacent leg and the hypotenuse. Both of these values ​​always have a value less than one, since the hypotenuse is always longer than the leg.

The tangent of an angle is a value equal to the ratio of the opposite leg to the adjacent leg of the desired angle, or sine to cosine. The cotangent, in turn, is the ratio of the adjacent leg of the desired angle to the opposite cactet. The cotangent of an angle can also be obtained by dividing the unit by the value of the tangent.

unit circle

A unit circle in geometry is a circle whose radius is equal to one. Such a circle is constructed in the Cartesian coordinate system, with the center of the circle coinciding with the origin point, and the initial position of the radius vector is determined by the positive direction of the X axis (abscissa axis). Each point of the circle has two coordinates: XX and YY, that is, the coordinates of the abscissa and ordinate. Selecting any point on the circle in the XX plane, and dropping the perpendicular from it to the abscissa axis, we get a right triangle formed by a radius to the selected point (let us denote it by the letter C), a perpendicular drawn to the X axis (the intersection point is denoted by the letter G), and a segment the abscissa axis between the origin (the point is denoted by the letter A) and the intersection point G. The resulting triangle ACG is a right triangle inscribed in a circle, where AG is the hypotenuse, and AC and GC are the legs. The angle between the radius of the circle AC and the segment of the abscissa axis with the designation AG, we define as α (alpha). So, cos α = AG/AC. Given that AC is the radius of the unit circle, and it is equal to one, it turns out that cos α=AG. Similarly, sin α=CG.

In addition, knowing these data, you can determine the coordinate of point C on the circle, since cos α=AG, and sin α=CG, which means that point C has the given coordinates (cos α; sin α). Knowing that the tangent is equal to the ratio of the sine to the cosine, we can determine that tg α \u003d y / x, and ctg α \u003d x / y. Considering the angles in a negative coordinate system, it can be calculated that the sine and cosine values ​​of some angles can be negative.

Calculations and basic formulas

Values ​​of trigonometric functions

Having considered the essence of trigonometric functions through the unit circle, we can derive the values ​​of these functions for some angles. The values ​​are listed in the table below.

The simplest trigonometric identities

Equations in which there is an unknown value under the sign of the trigonometric function are called trigonometric. Identities with the value sin x = α, k is any integer:

1. sin x = 0, x = πk.
2. 2. sin x \u003d 1, x \u003d π / 2 + 2πk.
3. sin x \u003d -1, x \u003d -π / 2 + 2πk.
4. sin x = a, |a| > 1, no solutions.
5. sin x = a, |a| ≦ 1, x = (-1)^k * arcsin α + πk.

Identities with the value cos x = a, where k is any integer:

1. cos x = 0, x = π/2 + πk.
2. cos x = 1, x = 2πk.
3. cos x \u003d -1, x \u003d π + 2πk.
4. cos x = a, |a| > 1, no solutions.
5. cos x = a, |a| ≦ 1, х = ±arccos α + 2πk.

Identities with the value tg x = a, where k is any integer:

1. tg x = 0, x = π/2 + πk.
2. tg x \u003d a, x \u003d arctg α + πk.

Identities with value ctg x = a, where k is any integer:

1. ctg x = 0, x = π/2 + πk.
2. ctg x \u003d a, x \u003d arcctg α + πk.

Cast formulas

This category of constant formulas denotes methods by which you can go from trigonometric functions of the form to functions of the argument, that is, convert the sine, cosine, tangent and cotangent of an angle of any value to the corresponding indicators of the angle of the interval from 0 to 90 degrees for greater convenience of calculations.

The formulas for reducing functions for the sine of an angle look like this:

• sin(900 - α) = α;
• sin(900 + α) = cos α;
• sin(1800 - α) = sin α;
• sin(1800 + α) = -sin α;
• sin(2700 - α) = -cos α;
• sin(2700 + α) = -cos α;
• sin(3600 - α) = -sin α;
• sin(3600 + α) = sin α.

For the cosine of an angle:

• cos(900 - α) = sin α;
• cos(900 + α) = -sin α;
• cos(1800 - α) = -cos α;
• cos(1800 + α) = -cos α;
• cos(2700 - α) = -sin α;
• cos(2700 + α) = sin α;
• cos(3600 - α) = cos α;
• cos(3600 + α) = cos α.

The use of the above formulas is possible subject to two rules. First, if the angle can be represented as a value (π/2 ± a) or (3π/2 ± a), the value of the function changes:

• from sin to cos;
• from cos to sin;
• from tg to ctg;
• from ctg to tg.

The value of the function remains unchanged if the angle can be represented as (π ± a) or (2π ± a).

Secondly, the sign of the reduced function does not change: if it was initially positive, it remains so. The same is true for negative functions.

Addition Formulas

These formulas express the values ​​of the sine, cosine, tangent, and cotangent of the sum and difference of two rotation angles in terms of their trigonometric functions. Angles are usually denoted as α and β.

The formulas look like this:

1. sin(α ± β) = sin α * cos β ± cos α * sin.
2. cos(α ± β) = cos α * cos β ∓ sin α * sin.
3. tan(α ± β) = (tan α ± tan β) / (1 ∓ tan α * tan β).
4. ctg(α ± β) = (-1 ± ctg α * ctg β) / (ctg α ± ctg β).

These formulas are valid for any angles α and β.

Double and triple angle formulas

The trigonometric formulas of a double and triple angle are formulas that relate the functions of the angles 2α and 3α, respectively, to the trigonometric functions of the angle α. Derived from addition formulas:

1. sin2α = 2sinα*cosα.
2. cos2α = 1 - 2sin^2α.
3. tg2α = 2tgα / (1 - tg^2 α).
4. sin3α = 3sinα - 4sin^3α.
5. cos3α = 4cos^3α - 3cosα.
6. tg3α = (3tgα - tg^3 α) / (1-tg^2 α).

Transition from sum to product

Considering that 2sinx*cosy = sin(x+y) + sin(x-y), simplifying this formula, we obtain the identity sinα + sinβ = 2sin(α + β)/2 * cos(α − β)/2. Similarly, sinα - sinβ = 2sin(α - β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα - cosβ = 2sin(α + β)/2 * sin(α − β)/2; tgα + tgβ = sin(α + β) / cosα * cosβ; tgα - tgβ = sin(α - β) / cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).

Transition from product to sum

These formulas follow from the identities for the transition of the sum to the product:

• sinα * sinβ = 1/2*;
• cosα * cosβ = 1/2*;
• sinα * cosβ = 1/2*.

Reduction Formulas

In these identities, the square and cubic powers of the sine and cosine can be expressed in terms of the sine and cosine of the first power of a multiple angle:

• sin^2 α = (1 - cos2α)/2;
• cos^2α = (1 + cos2α)/2;
• sin^3 α = (3 * sinα - sin3α)/4;
• cos^3 α = (3 * cosα + cos3α)/4;
• sin^4 α = (3 - 4cos2α + cos4α)/8;
• cos^4 α = (3 + 4cos2α + cos4α)/8.

Universal substitution

The universal trigonometric substitution formulas express trigonometric functions in terms of the tangent of a half angle.

• sin x \u003d (2tgx / 2) * (1 + tg ^ 2 x / 2), while x \u003d π + 2πn;
• cos x = (1 - tg^2 x/2) / (1 + tg^2 x/2), where x = π + 2πn;
• tg x \u003d (2tgx / 2) / (1 - tg ^ 2 x / 2), where x \u003d π + 2πn;
• ctg x \u003d (1 - tg ^ 2 x / 2) / (2tgx / 2), while x \u003d π + 2πn.

Special cases

Particular cases of the simplest trigonometric equations are given below (k is any integer).

Private for sine:

sin x value	x value
0	pk
1	π/2 + 2πk
-1	-π/2 + 2πk
1/2	π/6 + 2πk or 5π/6 + 2πk
-1/2	-π/6 + 2πk or -5π/6 + 2πk
√2/2	π/4 + 2πk or 3π/4 + 2πk
-√2/2	-π/4 + 2πk or -3π/4 + 2πk
√3/2	π/3 + 2πk or 2π/3 + 2πk
-√3/2	-π/3 + 2πk or -2π/3 + 2πk

Cosine quotients:

cos x value	x value
0	π/2 + 2πk
1	2πk
-1	2 + 2πk
1/2	±π/3 + 2πk
-1/2	±2π/3 + 2πk
√2/2	±π/4 + 2πk
-√2/2	±3π/4 + 2πk
√3/2	±π/6 + 2πk
-√3/2	±5π/6 + 2πk

Private for tangent:

tg x value	x value
0	pk
1	π/4 + πk
-1	-π/4 + πk
√3/3	π/6 + πk
-√3/3	-π/6 + πk
√3	π/3 + πk
-√3	-π/3 + πk

Cotangent quotients:

ctg x value	x value
0	π/2 + πk
1	π/4 + πk
-1	-π/4 + πk
√3	π/6 + πk
-√3	-π/3 + πk
√3/3	π/3 + πk
-√3/3	-π/3 + πk

Theorems

Sine theorem

There are two versions of the theorem - simple and extended. Simple sine theorem: a/sin α = b/sin β = c/sin γ. In this case, a, b, c are the sides of the triangle, and α, β, γ are the opposite angles, respectively.

Extended sine theorem for an arbitrary triangle: a/sin α = b/sin β = c/sin γ = 2R. In this identity, R denotes the radius of the circle in which the given triangle is inscribed.

Cosine theorem

The identity is displayed in this way: a^2 = b^2 + c^2 - 2*b*c*cos α. In the formula, a, b, c are the sides of the triangle, and α is the angle opposite side a.

Tangent theorem

The formula expresses the relationship between the tangents of two angles, and the length of the sides opposite them. The sides are labeled a, b, c, and the corresponding opposite angles are α, β, γ. The formula of the tangent theorem: (a - b) / (a+b) = tg((α - β)/2) / tg((α + β)/2).

Cotangent theorem

Associates the radius of a circle inscribed in a triangle with the length of its sides. If a, b, c are the sides of a triangle, and A, B, C, respectively, are their opposite angles, r is the radius of the inscribed circle, and p is the half-perimeter of the triangle, the following identities hold:

• ctg A/2 = (p-a)/r;
• ctg B/2 = (p-b)/r;
• ctg C/2 = (p-c)/r.

Applications

Trigonometry is not only a theoretical science associated with mathematical formulas. Its properties, theorems and rules are used in practice by various branches of human activity - astronomy, air and sea navigation, music theory, geodesy, chemistry, acoustics, optics, electronics, architecture, economics, mechanical engineering, measuring work, computer graphics, cartography, oceanography, and many others.

Sine, cosine, tangent and cotangent are the basic concepts of trigonometry, with which you can mathematically express the relationship between angles and lengths of sides in a triangle, and find the desired quantities through identities, theorems and rules.

Trigonometric equations are not the easiest topic. Painfully they are diverse.) For example, these:

sin2x + cos3x = ctg5x

sin(5x+π /4) = ctg(2x-π /3)

sinx + cos2x + tg3x = ctg4x

Etc...

But these (and all other) trigonometric monsters have two common and obligatory features. First - you won't believe it - there are trigonometric functions in the equations.) Second: all expressions with x are within these same functions. And only there! If x appears somewhere outside, For example, sin2x + 3x = 3, this will be a mixed type equation. Such equations require an individual approach. Here we will not consider them.

We will not solve evil equations in this lesson either.) Here we will deal with the simplest trigonometric equations. Why? Yes, because the decision any trigonometric equations consists of two stages. At the first stage, the evil equation is reduced to a simple one by various transformations. On the second - this simplest equation is solved. No other way.

So, if you have problems in the second stage, the first stage does not make much sense.)

What do elementary trigonometric equations look like?

sinx = a

cosx = a

tgx = a

ctgx = a

Here a stands for any number. Any.

By the way, inside the function there may be not a pure x, but some kind of expression, such as:

cos(3x+π /3) = 1/2

etc. This complicates life, but does not affect the method of solving the trigonometric equation.

How to solve trigonometric equations?

Trigonometric equations can be solved in two ways. The first way: using logic and a trigonometric circle. We will explore this path here. The second way - using memory and formulas - will be considered in the next lesson.

The first way is clear, reliable, and hard to forget.) It is good for solving trigonometric equations, inequalities, and all sorts of tricky non-standard examples. Logic is stronger than memory!

We solve equations using a trigonometric circle.

We include elementary logic and the ability to use a trigonometric circle. Can't you!? However... It will be difficult for you in trigonometry...) But it doesn't matter. Take a look at the lessons "Trigonometric circle ...... What is it?" and "Counting angles on a trigonometric circle." Everything is simple there. Unlike textbooks...)

Ah, you know!? And even mastered "Practical work with a trigonometric circle"!? Accept congratulations. This topic will be close and understandable to you.) What is especially pleasing is that the trigonometric circle does not care which equation you solve. Sine, cosine, tangent, cotangent - everything is the same for him. The solution principle is the same.

So we take any elementary trigonometric equation. At least this:

cosx = 0.5

I need to find X. Speaking in human language, you need find the angle (x) whose cosine is 0.5.

How did we use the circle before? We drew a corner on it. In degrees or radians. And immediately seen trigonometric functions of this angle. Now let's do the opposite. Draw a cosine equal to 0.5 on the circle and immediately we'll see injection. It remains only to write down the answer.) Yes, yes!

We draw a circle and mark the cosine equal to 0.5. On the cosine axis, of course. Like this:

Now let's draw the angle that this cosine gives us. Hover your mouse over the picture (or touch the picture on a tablet), and see this same corner X.

Which angle has a cosine of 0.5?

x \u003d π / 3

cos 60°= cos( π /3) = 0,5

Some people will grunt skeptically, yes... They say, was it worth it to fence the circle, when everything is clear anyway... You can, of course, grunt...) But the fact is that this is an erroneous answer. Or rather, inadequate. Circle connoisseurs understand that there are still a whole bunch of angles that also give a cosine equal to 0.5.

If you turn the movable side OA for a full turn, point A will return to its original position. With the same cosine equal to 0.5. Those. the angle will change 360° or 2π radians, and cosine is not. The new angle 60° + 360° = 420° will also be a solution to our equation, because

There are an infinite number of such full rotations... And all these new angles will be solutions to our trigonometric equation. And they all need to be written down somehow. All. Otherwise, the decision is not considered, yes ...)

Mathematics can do this simply and elegantly. In one short answer, write down infinite set solutions. Here's what it looks like for our equation:

x = π /3 + 2π n, n ∈ Z

I will decipher. Still write meaningfully nicer than stupidly drawing some mysterious letters, right?)

π /3 is the same angle that we saw on the circle and determined according to the table of cosines.

2π is one full turn in radians.

n - this is the number of complete, i.e. whole revolutions. It is clear that n can be 0, ±1, ±2, ±3.... and so on. As indicated by the short entry:

n ∈ Z

n belongs ( ∈ ) to the set of integers ( Z ). By the way, instead of the letter n letters can be used k, m, t etc.

This notation means that you can take any integer n . At least -3, at least 0, at least +55. What do you want. If you plug that number into your answer, you get a specific angle, which is sure to be the solution to our harsh equation.)

Or, in other words, x \u003d π / 3 is the only root of an infinite set. To get all the other roots, it is enough to add any number of full turns to π / 3 ( n ) in radians. Those. 2πn radian.

Everything? No. I specifically stretch the pleasure. To remember better.) We received only a part of the answers to our equation. I will write this first part of the solution as follows:

x 1 = π /3 + 2π n, n ∈ Z

x 1 - not one root, it is a whole series of roots, written in short form.

But there are other angles that also give a cosine equal to 0.5!

Let's return to our picture, according to which we wrote down the answer. Here she is:

Move the mouse over the image and see another corner that also gives a cosine of 0.5. What do you think it equals? The triangles are the same... Yes! It is equal to the angle X , only plotted in the negative direction. This is the corner -X. But we have already calculated x. π /3 or 60°. Therefore, we can safely write:

x 2 \u003d - π / 3

And, of course, we add all the angles that are obtained through full turns:

x 2 = - π /3 + 2π n, n ∈ Z

That's all now.) In a trigonometric circle, we saw(who understands, of course)) all angles that give a cosine equal to 0.5. And they wrote down these angles in a short mathematical form. The answer is two infinite series of roots:

x 1 = π /3 + 2π n, n ∈ Z

x 2 = - π /3 + 2π n, n ∈ Z

This is the correct answer.

Hope, general principle for solving trigonometric equations with the help of a circle is understandable. We mark the cosine (sine, tangent, cotangent) from the given equation on the circle, draw the corresponding angles and write down the answer. Of course, you need to figure out what kind of corners we are saw on the circle. Sometimes it's not so obvious. Well, as I said, logic is required here.)

For example, let's analyze another trigonometric equation:

Please note that the number 0.5 is not the only possible number in the equations!) It's just more convenient for me to write it than roots and fractions.

We work according to the general principle. We draw a circle, mark (on the sine axis, of course!) 0.5. We draw at once all the angles corresponding to this sine. We get this picture:

Let's deal with the angle first. X in the first quarter. We recall the table of sines and determine the value of this angle. The matter is simple:

x \u003d π / 6

We recall the full turns and, with a clear conscience, write down the first series of answers:

x 1 = π /6 + 2π n, n ∈ Z

Half the job is done. Now we need to define second corner... This is trickier than in cosines, yes ... But logic will save us! How to determine the second angle through x? Yes Easy! The triangles in the picture are the same, and the red corner X equal to the angle X . Only it is counted from the angle π in the negative direction. That's why it's red.) And for our answer, we need an angle measured correctly from the positive semiaxis OX, i.e. from an angle of 0 degrees.

Hover the cursor over the picture and see everything. I removed the first corner so as not to complicate the picture. The angle of interest to us (drawn in green) will be equal to:

π - x

x we know it π /6 . So the second angle will be:

π - π /6 = 5π /6

Again, we recall the addition of full revolutions and write down the second series of answers:

x 2 = 5π /6 + 2π n, n ∈ Z

That's all. A complete answer consists of two series of roots:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Equations with tangent and cotangent can be easily solved using the same general principle for solving trigonometric equations. Unless, of course, you know how to draw the tangent and cotangent on a trigonometric circle.

In the examples above, I used the tabular value of sine and cosine: 0.5. Those. one of those meanings that the student knows must. Now let's expand our capabilities to all other values. Decide, so decide!)

So, let's say we need to solve the following trigonometric equation:

There is no such value of the cosine in the short tables. We coolly ignore this terrible fact. We draw a circle, mark 2/3 on the cosine axis and draw the corresponding angles. We get this picture.

We understand, for starters, with an angle in the first quarter. To know what x is equal to, they would immediately write down the answer! We don't know... Failure!? Calm! Mathematics does not leave its own in trouble! She invented arc cosines for this case. Do not know? In vain. Find out. It's a lot easier than you think. According to this link, there is not a single tricky spell about "inverse trigonometric functions" ... It's superfluous in this topic.

If you're in the know, just say to yourself, "X is an angle whose cosine is 2/3." And immediately, purely by definition of the arccosine, we can write:

We remember about additional revolutions and calmly write down the first series of roots of our trigonometric equation:

x 1 = arccos 2/3 + 2π n, n ∈ Z

The second series of roots is also written almost automatically, for the second angle. Everything is the same, only x (arccos 2/3) will be with a minus:

x 2 = - arccos 2/3 + 2π n, n ∈ Z

And all things! This is the correct answer. Even easier than with tabular values. You don’t need to remember anything.) By the way, the most attentive will notice that this picture with the solution through the arc cosine is essentially no different from the picture for the equation cosx = 0.5.

Exactly! The general principle on that and the general! I specifically drew two almost identical pictures. The circle shows us the angle X by its cosine. It is a tabular cosine, or not - the circle does not know. What kind of angle is this, π / 3, or what kind of arc cosine is up to us to decide.

With a sine the same song. For example:

Again we draw a circle, mark the sine equal to 1/3, draw the corners. It turns out this picture:

And again the picture is almost the same as for the equation sinx = 0.5. Again we start from the corner in the first quarter. What is x equal to if its sine is 1/3? No problem!

So the first pack of roots is ready:

x 1 = arcsin 1/3 + 2π n, n ∈ Z

Let's take a look at the second angle. In the example with a table value of 0.5, it was equal to:

π - x

So here it will be exactly the same! Only x is different, arcsin 1/3. So what!? You can safely write the second pack of roots:

x 2 = π - arcsin 1/3 + 2π n, n ∈ Z

This is a completely correct answer. Although it does not look very familiar. But it's understandable, I hope.)

This is how trigonometric equations are solved using a circle. This path is clear and understandable. It is he who saves in trigonometric equations with the selection of roots on a given interval, in trigonometric inequalities - they are generally solved almost always in a circle. In short, in any tasks that are a little more complicated than standard ones.

Putting knowledge into practice?

Solve trigonometric equations:

At first it is simpler, directly on this lesson.

Now it's more difficult.

Hint: here you have to think about the circle. Personally.)

And now outwardly unpretentious ... They are also called special cases.

sinx = 0

sinx = 1

cosx = 0

cosx = -1

Hint: here you need to figure out in a circle where there are two series of answers, and where there is one ... And how to write down one instead of two series of answers. Yes, so that not a single root from an infinite number is lost!)

Well, quite simple):

sinx = 0,3

cosx = π

tgx = 1,2

ctgx = 3,7

Hint: here you need to know what is the arcsine, arccosine? What is arc tangent, arc tangent? The simplest definitions. But you don’t need to remember any tabular values!)

The answers are, of course, in disarray):

x 1= arcsin0,3 + 2πn, n ∈ Z
x 2= π - arcsin0.3 + 2

Not everything works out? It happens. Read the lesson again. Only thoughtfully(there is such an obsolete word...) And follow the links. The main links are about the circle. Without it in trigonometry - how to cross the road blindfolded. Sometimes it works.)

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

Trigonometric equations .

The simplest trigonometric equations .

Methods for solving trigonometric equations.

Trigonometric equations. An equation containing an unknown under the sign of the trigonometric function is called trigonometric.

The simplest trigonometric equations.

Methods for solving trigonometric equations. The solution of the trigonometric equation consists of two stages: equation transformation to get it simple type (see above) and decisionobtained simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.

1. Algebraic method. This method is well known to us from algebra

(variable substitution and substitution method).

2. Factorization. Let's look at this method with examples.

EXAMPLE 1. Solve the equation: sin x+ cos x = 1 .

Solution. Move all terms of the equation to the left:

Sin x+ cos x – 1 = 0 ,

Let us transform and factorize the expression in

Left side of the equation:

Example 2. Solve the equation: cos 2 x+ sin x cos x = 1.

SOLUTION cos 2 x+ sin x cos x– sin 2 x– cos 2 x = 0 ,

Sin x cos x– sin 2 x = 0 ,

Sin x(cos x– sin x ) = 0 ,

Example 3. Solve the equation: cos 2 x– cos 8 x+ cos 6 x = 1.

SOLUTION cos 2 x+ cos 6 x= 1 + cos8 x,

2 cos 4 x cos 2 x= 2 cos² 4 x ,

Cos 4 x · (cos 2 x– cos 4 x) = 0 ,

Cos 4 x 2 sin 3 x sin x = 0 ,

one). cos 4 x= 0 , 2). sin 3 x= 0 , 3). sin x = 0 ,

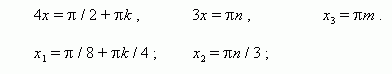
3.

Casting to uniform equation. The equation called homogeneous from relatively sin and cos , if all of it terms of the same degree with respect to sin and cos the same angle. To solve a homogeneous equation, you need: a) move all its members to the left side; b) put all common factors out of brackets; in) equate all factors and brackets to zero; G) parentheses set to zero give homogeneous equation of lesser degree, which should be divided by cos(or sin) in the senior degree; d) solve the resulting algebraic equation with respect totan . EXAMPLE Solve Equation: 3 sin 2 x+ 4 sin x cos x+ 5 cos 2 x = 2. Solution: 3sin 2 x+ 4 sin x cos x+ 5 cos 2 x= 2 sin 2 x+ 2 cos 2 x , Sin 2 x+ 4 sin x cos x+ 3 cos 2 x = 0 , Tan 2 x+ 4tan x + 3 = 0 , from here y 2 + 4y +3 = 0 , The roots of this equation are:y 1 = - 1, y 2 = - 3, hence 1) tan x= –1, 2) tan x = –3,

4. Transition to half corner. Let's look at this method with an example:

EXAMPLE Solve Equation: 3 sin x– 5cos x = 7.

Solution: 6 sin ( x/ 2) cos ( x/ 2) – 5 cos² ( x/ 2) + 5 sin² ( x/ 2) =

7 sin² ( x/ 2) + 7 cos² ( x/ 2) ,

2 sin² ( x/ 2) – 6 sin ( x/ 2) cos ( x/ 2) + 12 cos² ( x/ 2) = 0 ,

tan² ( x/ 2) – 3 tan ( x/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introduction of an auxiliary angle. Consider an equation of the form:

a sin x + b cos x = c ,

Where a, b, c– coefficients;x- unknown.

Now the coefficients of the equation have the properties of sine and cosine, namely: module (absolute value) of each

The simplest trigonometric equations are the equations

Cos(x)=a, sin(x)=a, tg(x)=a, ctg(x)=a

Equation cos(x) = a

Explanation and rationale

1. The roots of the equation cosx = a. When | a | > 1 the equation has no roots because | cosx |< 1 для любого x (прямая y = а при а >1 or at a< -1 не пересекает график функцииy = cosx).

Let | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. On the interval, the function y = cos x decreases from 1 to -1. But a decreasing function takes each of its values ​​​​only at one point of its domain of definition, therefore the equation cos x \u003d a has only one root on this interval, which, by definition of the arc cosine, is: x 1 \u003d arccos a (and for this root cos x \u003d a).

Cosine is an even function, so on the interval [-n; 0] the equation cos x = and also has only one root - the number opposite to x 1, that is

x 2 = -arccos a.

Thus, on the interval [-n; n] (length 2n) the equation cos x = a for | a |< 1 имеет только корни x = ±arccos а.

The function y = cos x is periodic with a period of 2n, so all other roots differ from those found by 2np (n € Z). We get the following formula for the roots of the equation cos x = a when

x = ± arccos a + 2n, n £ Z.

1. Particular cases of solving the equation cosx = a.

It is useful to remember the special notation for the roots of the equation cos x = a when

a \u003d 0, a \u003d -1, a \u003d 1, which can be easily obtained using the unit circle as a guide.

Since the cosine is equal to the abscissa of the corresponding point on the unit circle, we get that cos x = 0 if and only if the corresponding point on the unit circle is point A or point B.

Similarly, cos x = 1 if and only if the corresponding point of the unit circle is the point C, therefore,

x = 2πp, k € Z.

Also cos x \u003d -1 if and only if the corresponding point of the unit circle is the point D, thus x \u003d n + 2n,

Equation sin(x) = a

Explanation and rationale

1. The roots of the equation sinx = a. When | a | > 1 the equation has no roots because | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 or at a< -1 не пересекает график функции y = sinx).

Lesson and presentation on the topic: "Solution of the simplest trigonometric equations"

Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions! All materials are checked by an antivirus program.

Manuals and simulators in the online store "Integral" for grade 10 from 1C
We solve problems in geometry. Interactive tasks for building in space
Software environment "1C: Mathematical constructor 6.1"

What will we study:
1. What are trigonometric equations?

3. Two main methods for solving trigonometric equations.
4. Homogeneous trigonometric equations.
5. Examples.

What are trigonometric equations?

Guys, we have already studied the arcsine, arccosine, arctangent and arccotangent. Now let's look at trigonometric equations in general.

Trigonometric equations - equations in which the variable is contained under the sign of the trigonometric function.

We repeat the form of solving the simplest trigonometric equations:

1) If |а|≤ 1, then the equation cos(x) = a has a solution:

X= ± arccos(a) + 2πk

2) If |а|≤ 1, then the equation sin(x) = a has a solution:

3) If |a| > 1, then the equation sin(x) = a and cos(x) = a have no solutions 4) The equation tg(x)=a has a solution: x=arctg(a)+ πk

5) The equation ctg(x)=a has a solution: x=arcctg(a)+ πk

For all formulas, k is an integer

The simplest trigonometric equations have the form: Т(kx+m)=a, T- any trigonometric function.

Example.

Solve equations: a) sin(3x)= √3/2

Decision:

A) Let's denote 3x=t, then we will rewrite our equation in the form:

The solution to this equation will be: t=((-1)^n)arcsin(√3/2)+ πn.

From the table of values ​​we get: t=((-1)^n)×π/3+ πn.

Let's go back to our variable: 3x =((-1)^n)×π/3+ πn,

Then x= ((-1)^n)×π/9+ πn/3

Answer: x= ((-1)^n)×π/9+ πn/3, where n is an integer. (-1)^n - minus one to the power of n.

More examples of trigonometric equations.

Solve the equations: a) cos(x/5)=1 b)tg(3x- π/3)= √3

Decision:

A) This time we will go directly to the calculation of the roots of the equation right away:

X/5= ± arccos(1) + 2πk. Then x/5= πk => x=5πk

Answer: x=5πk, where k is an integer.

B) We write in the form: 3x- π/3=arctg(√3)+ πk. We know that: arctg(√3)= π/3

3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

Answer: x=2π/9 + πk/3, where k is an integer.

Solve equations: cos(4x)= √2/2. And find all the roots on the segment .

Decision:

Let's solve our equation in general form: 4x= ± arccos(√2/2) + 2πk

4x= ± π/4 + 2πk;

X= ± π/16+ πk/2;

Now let's see what roots fall on our segment. For k For k=0, x= π/16, we are in the given segment .
With k=1, x= π/16+ π/2=9π/16, they hit again.
For k=2, x= π/16+ π=17π/16, but here we didn’t hit, which means we won’t hit for large k either.

Answer: x= π/16, x= 9π/16

Two main solution methods.

We have considered the simplest trigonometric equations, but there are more complex ones. To solve them, the method of introducing a new variable and the factorization method are used. Let's look at examples.

Let's solve the equation:

Decision:
To solve our equation, we use the method of introducing a new variable, denoted: t=tg(x).

As a result of the replacement, we get: t 2 + 2t -1 = 0

Find the roots of the quadratic equation: t=-1 and t=1/3

Then tg(x)=-1 and tg(x)=1/3, we got the simplest trigonometric equation, let's find its roots.

X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

Answer: x= -π/4+πk; x=arctg(1/3) + πk.

An example of solving an equation

Solve equations: 2sin 2 (x) + 3 cos(x) = 0

Decision:

Let's use the identity: sin 2 (x) + cos 2 (x)=1

Our equation becomes: 2-2cos 2 (x) + 3 cos (x) = 0

2 cos 2 (x) - 3 cos(x) -2 = 0

Let's introduce the replacement t=cos(x): 2t 2 -3t - 2 = 0

The solution to our quadratic equation are the roots: t=2 and t=-1/2

Then cos(x)=2 and cos(x)=-1/2.

Because cosine cannot take values ​​greater than one, then cos(x)=2 has no roots.

For cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

Answer: x= ±2π/3 + 2πk

Homogeneous trigonometric equations.

Definition: An equation of the form a sin(x)+b cos(x) is called homogeneous trigonometric equations of the first degree.

Equations of the form

homogeneous trigonometric equations of the second degree.

To solve a homogeneous trigonometric equation of the first degree, we divide it by cos(x): It is impossible to divide by cosine if it is equal to zero, let's make sure that this is not so:
Let cos(x)=0, then asin(x)+0=0 => sin(x)=0, but sine and cosine are not equal to zero at the same time, we got a contradiction, so we can safely divide by zero.

Solve the equation:
Example: cos 2 (x) + sin(x) cos(x) = 0

Decision:

Take out the common factor: cos(x)(c0s(x) + sin (x)) = 0

Then we need to solve two equations:

cos(x)=0 and cos(x)+sin(x)=0

Cos(x)=0 for x= π/2 + πk;

Consider the equation cos(x)+sin(x)=0 Divide our equation by cos(x):

1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

Answer: x= π/2 + πk and x= -π/4+πk

How to solve homogeneous trigonometric equations of the second degree?
Guys, stick to these rules always!

1. See what the coefficient a is equal to, if a \u003d 0 then our equation will take the form cos (x) (bsin (x) + ccos (x)), an example of the solution of which is on the previous slide

2. If a≠0, then you need to divide both parts of the equation by the squared cosine, we get:

We make the change of variable t=tg(x) we get the equation:

Solve Example #:3

Solve the equation:
Decision:

Divide both sides of the equation by cosine square:

We make a change of variable t=tg(x): t 2 + 2 t - 3 = 0

Find the roots of the quadratic equation: t=-3 and t=1

Then: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

Tg(x)=1 => x= π/4+ πk

Answer: x=-arctg(3) + πk and x= π/4+ πk

Solve Example #:4

Solve the equation:

Decision:
Let's transform our expression:

We can solve such equations: x= - π/4 + 2πk and x=5π/4 + 2πk

Answer: x= - π/4 + 2πk and x=5π/4 + 2πk

Solve Example #:5

Solve the equation:

Decision:
Let's transform our expression:

We introduce the replacement tg(2x)=t:2 2 - 5t + 2 = 0

The solution to our quadratic equation will be the roots: t=-2 and t=1/2

Then we get: tg(2x)=-2 and tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

Answer: x=-arctg(2)/2 + πk/2 and x=arctg(1/2)/2+ πk/2

Tasks for independent solution.

1) Solve the equation

A) sin(7x)= 1/2 b) cos(3x)= √3/2 c) cos(-x) = -1 d) tg(4x) = √3 e) ctg(0.5x) = -1.7

2) Solve equations: sin(3x)= √3/2. And find all the roots on the segment [π/2; π].

3) Solve the equation: ctg 2 (x) + 2ctg(x) + 1 =0

4) Solve the equation: 3 sin 2 (x) + √3sin (x) cos(x) = 0

5) Solve the equation: 3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

6) Solve the equation: cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)